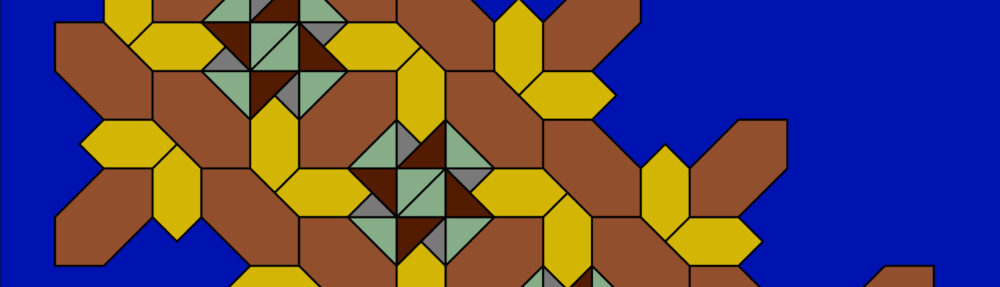
Depuis quelque temps je travaille sur les formes des zelliges arabo-andalouses de la forme la plus simple (le triangle) à celles les plus complètes ou complexes (étoiles avec un grand nombre de branches ou formes complexes symétriques ou non symétriques par exemple).

Vous pouvez voir ici le début d’un travail préliminaire sur ces principes.

(dans cet article vous m’excuserez de l’absence de notation mathématique formelle, je ne suis pas mathématicien et n’utilise les mathématiques que pour formuler une idée. de plus je pense qu’il me faudrait un plugin spécifique afin de noter correctement les concepts dont je parle… et aussi peut-être à mieux les expliquer. La porte est ouverte à qui veut l’aider dans cette tâche).

En apprenant à dessiner les formes de pièces de zelliges utilisées dans la création des céramiques murales d’Espagne et du Maroc mais aussi de la plupart des pays influencés par ces décorations, je me suis aperçu de deux constantes : l’usage du carré de 2 et de la racine carré de 2 et l’usage d’angles précis dans la majorité des cas (exception pour l’exemple d’étoiles avec de nombreuses branches).

Quand on veut dessiner une pièce de zellige, on va se retrouver à faire des calculs sur la longueur des cotés et pour cela on doit connaître aussi les angles entre ses cotés. La plupart de ces angles sont des multiples de 15 degrés alors que la longueur des cotés est une valeur de base multipliée ou divisée par un nombre en rapport avec la racine carrée de deux.

Un autre point important pour définir une zellige est son centre de gravité. Autant il est facile à trouver pour une forme simple (style carré ou rectangle) ou la plupart des formes symétriques sur les deux axes autant il nécessitera un calcul complexe sur des formes symétriques sur un axe ou alors complètement asymétriques mais on y reviendra dans un autre article car je ne sais pas encore l’incidence du centre de gravité d’une pièce sur son rapport à la musique.

Une deuxième façon de procéder serait au contraire de trouver plus ou moins intuitivement par la présence d’un réseau de cercles entourant chaque point ce centre de gravité ou du moins le centre commun de toutes ces pièces puisqu’en l’état ce point serait central de la pièce (et peut-être pas son centre de gravité) et serait défini par l’ensemble des rayons de ces cercles ayant ce point commun sur leurs cercles respectifs. J’espère que vous me suivez. Un mathématicien me serait bien utile pour expliquer cela.

Par contre dès la création de ce centre (de gravité ou non) — ou du moins le calcul de sa valeur — il permettra de calculer entre ce point et l’ensemble des sommets des cotés, la longueur de chacun de ces segments et chaque longueur correspondra à une fréquence dès qu’on aura donné la longueur du la de base. exemple : si on a un carré ABCD de 100 points de coté son centre G est de 50 en x et de 50 en y. On a donc la longueur de chaque segment du centre aux sommets GA, GB, GC, GD égale la moitié de la racine carré de AB2 + BC2 soit approximativement 70,71 pts. Dans cet exemple, si une longueur de 50 pts égale la fréquence du la alors pour trouver la fréquence des sommets il suffira de faire l’opération suivante 70,71 / 50 * 440 hz soit 622,248 hz soit la note de ré dièse ou mi bémol de l’octave au-dessus. Plus simplement, il suffira de calculer le rapport entre la valeur du segment de base et du segment visé pour obtenir cette note. Ces rapports peuvent être notés de la façon suivante : on prend 2 racine de 12 qu’on met à la puissance n avec n égale de 1 à 12 et qu’on multiplie par la fréquence de la note de départ pour obtenir la fréquence juste des notes de l’octave concernée.

Pourquoi ce calcul ? Pourquoi 2 racine de 12 et pas autre chose ?

Simplement parce qu’il y a douze notes par octave et que le rapport d’une note avec la même note à l’octave est de deux. L’écart de fréquences restant constant pour la gamme tempérée, celui-ci est donc de la fréquence de la note multipliée par la racine douzième de 2 pour obtenir la fréquence de la note suivante. Pour le reste il faut se fier à ce qui a déjà été calculé par des scientifiques et/ou des théoriciens du son et de la musique sans trop se poser de questions. Malgré tout je peux vous dire que ce n’est pas le cas dans les gammes et tempéraments plus exotiques ou de factures très anciennes… et que certains instruments n’ayant pas de frettes comme le violon et ses grands frères et grandes sœurs échappent à cette contrainte. D’autres comme le sitar ont des frettes amovibles permettant de modifier la gamme jouée et de s’adapter ainsi à l’atmosphère du morceau que l’on veut interpréter. C’est spécifique de la musique indienne dont l’élaboration des gammes est spécifique à chaque musicien mais avec un système de codification très sophistiqué.

Bon, revenons à nos moutons. pour nos exemples, on prendra comme référence que l’octave 3 est l’octave où se trouve le la du diapason. Les octaves audibles ayant donc les valeurs de -1 à +9.

exemples :

• le la de l’octave 3 vaut 440 hertz
• le la dièse (ou si bémol) vaudra 440 x 2 racine de 12 puissance 1 égalera approximativement 466,164 hz
• le si vaudra 440 x 2 racine de 12 puissance 2 égalera approximativement 493,883 hz
• le do vaudra 440 x 2 racine de 12 puissance 3 égalera approximativement 523,251 hz
• etc, etc 
• jusqu’au la de l’octave au-dessus qui vaudra 440 x 2 racine de 12 puissance 12 égalera 880 hz

On peut continuer d’augmenter le n mis en indice des puissances pour obtenir des notes à l’infini :

• le la de la cinquième octave sera donc calculé ainsi 440 x 2 racine de 12 puissance 24 soit 1760 hz
• le la de sixième octave : 3520 hz avec n = 36
• septième octave : 7040 hz et n = 48
• huitième octave : 14080 hz et n = 60
• neuvième octave : 28160 hz et n = 72

On arrive là dans les ultra-sons puisque l’oreille humaine n’est capable que d’entendre des bruits jusqu’à environ 20 000 hz et ce pour les meilleures auditions. L’intensité du son joue bien sûr aussi en ce sens et un son de forte intensité d’une certaine fréquence s’entendra d’autant mieux qu’il couvrira les autres bruits présents et que l’auditeur est dur d’oreille comme on dit.

Pour obtenir la valeur hertzienne des notes sous le la de base il suffit de diviser plutôt que de multiplier et le tour est joué.

exemple

• le la de l’octave 2 vaudra 440 / 2 racine de 12 puissance 12 et égalera 220 hertz
• le do juste au-dessus vaudra 440 / 2 racine de 12 puissance 9 et égalera 261,625 hertz

En résumé on pourra donc jouer les notes suivant la position dans l’espace des sommets d’un polygone régulier ou irrégulier.

Pour l’ordre dans lequel ces notes seront jouées, il suffira de faire tourner dans le sens des aiguilles d’une montre un axe partant du centre de cet objet et tournant à une vitesse donné. Cette vitesse correspondra au tempo de l’objet musical représenté par le polygone. A chaque tour on revient au point de départ. On a donc une boucle rythmique temporelle.

Si on prend une forme carrée, on aura donc 4 notes identiques si on prend le centre de ce carré comme point de départ de l’axe de rotation. Par contre, si on décale la zellige dans l’espace pour dissocier les deux points alors les notes représentées par les sommets du carré ne seront plus les même et donc en dessinant d’autres objets dans un espace infini, on pourra obtenir des notes différentes sur chaque objet représenté suivant les règles de départs donnés à ces objets.

exemples :

• un triangle équilatéral dont les segments sont tous identiques et de 50 points (donc correspondant à la note la et la fréquence de 440 hz ) et dont le point de bascule de l’axe de boucle est le centre de gravité de ce triangle jouera pour un tempo de 60 un la toutes les 1 seconde.
• pour un carré au même tempo mais avec des segments différents de 70,71 points on obtiendra un mi bémol toutes les exactement 3/4 secondes.
• Si pour ces deux objets on décale le point de bascule temporal on obtiendra alors des segments ayant des longueurs différentes mais aussi des angles différents la boucle aura donc un aspect très différent lorsqu’on la joue. De même si on reste mais qu’on déplace les sommets des segments.

La reproduction de ces mouvements mécaniques associés à un synthétiseur analogique pourrait être intéressant.

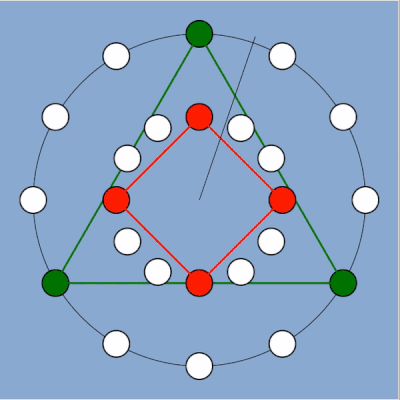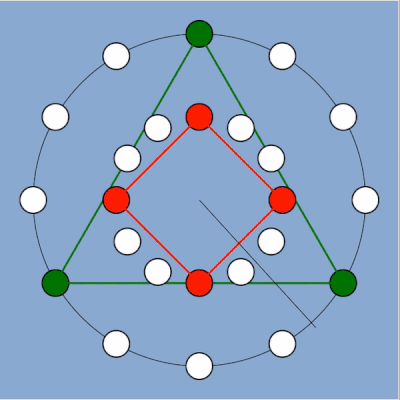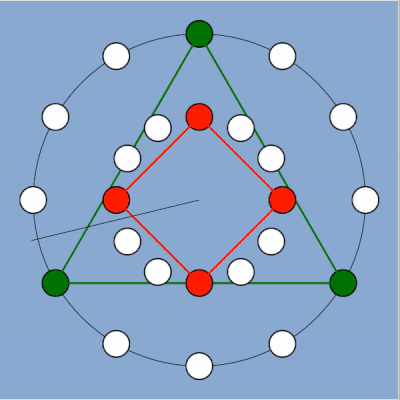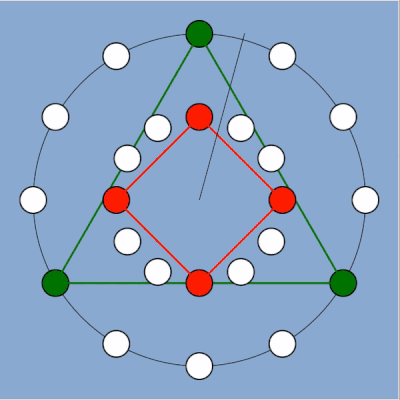
Vue d’un rythme eucliden (nous y reviendrons) correspondant pour partie aux exemples précédents ici les notes du triangle sont une octave au-dessus de celle du carré le rythme est en 3/4 ou 4/3 suivant qu’on prenne comme base l’un ou l’autre des deux instruments. Le tempo est en conséquence de ces paramètres.

Pour en revenir avec nos arpèges puisque là est le sujet de cet article.

Pour faire un arpège des notes do3–mi3–sol3 et que la base pour un la3 est un segment Gn valant 50 points alors il faudra que nos segments GA, GB et GC aient respectivement une longueur de :

• GA = 50 / 2 racine 12 puissance 9 soit 29,730 points
• GB = 50 / 2 racine 12 puissance  5 soit 37,457 points
• GB = 50 / 2 racine 12 puissance  2 soit 44,545 points

et rapportés aux fréquences on obtient

• fA = 29,730 / 50 x 440 hz = 261,625 hz
• fB = 37,457 / 50 x 440 hz = 329,622 hz
• fC = 44,545 / 50 x 440 hz = 391,996 hz

Ce qui correspond bien aux fréquences de nos trois notes.

Quand à leurs positions dans l’espace, on sait que cet arpège est joué à une note par temps (une noire), on aura donc les angles des segments pris deux par deux identiques à 120 degrés. Pour modifier la mélodie il suffira de modifier ses angles sans changer la longueur des segments pour conserver les même notes. L’addition des trois angles devant faire obligatoirement 360 degrés pour boucler la boucle. À l’inverse on pourra aussi modifier les longueurs des segments sans changer les angles pour obtenir une mélodie identique au niveau du tempo mais avec des notes, une gamme différentes.

Si la somme des trois angles est inférieure à 360 degrés (et encore faudra-t-il trouver une façon de le représenter par un mouvement de la zellige dans l’espace) on aura un arpège qui ira plus vite dans le temps donc un tempo plus rapide. Si c’est l’inverse alors on aura un tempo plus lent. Ces deux méthodes créeront donc si elles sont jouées indépendant un effet de tempo plus ou moins rapides: Par contre si elles sont mélangées à d’autres sons, d’autres motifs cela créera un effet d’avance ou de retard par rapport au tempo de base.

Suivant la forme des zelliges on obtiendra des arpèges ou des mélodies simples et répétitives suivant les différents critères utilisés :

forme de la zellige, polygone régulier ou irrégulier, angles aigus ou obtus, nombres de sommets, formes ramassées ou longues, zelliges avec des motifs symétriques ou non, point de départ du motif, etc.

Si on veut utiliser ces motifs dans une création musicale, il faudra trouver une manière de les assembler sur une même page et de définir indépendamment ou pour l’ensemble des zelliges des règles de jeux.

A établir dans une autre article …