Dans l’article précédent « Rapport entre la forme d’une zellige arabo-andalouse et d’un pattern musical (1ère partie) » J’ai commencé à expliquer comment les formes des zelliges arabo-andalouses pouvaient être utilisées pour interpréter une mélodie ou un rythme basés sur leur forme mathématique.

J’ai donné l’exemple d’un triangle et d’un carré circonscrit dans des cercles en rapport avec des notes de musique. Aujourd’hui je continue mon explication.

Je vais partir d’une simple étoile à 8 branches utilisée couramment dans les zelliges.

La voici.

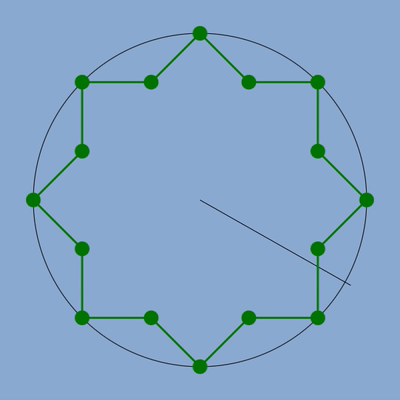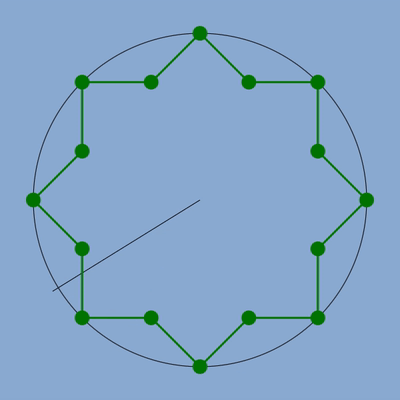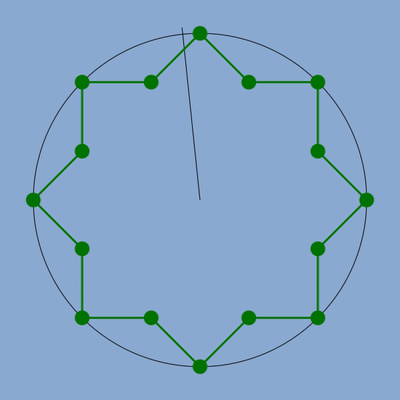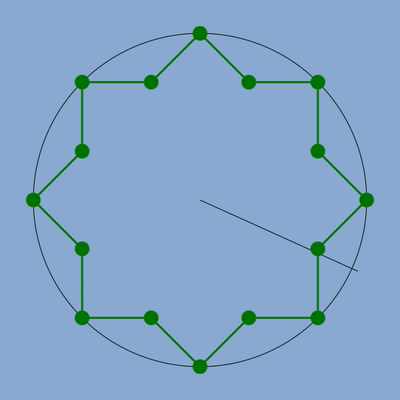
Cette étoile comme le motif avec triangle et carré du précédent article a été écrit en SVG et je commence à partir d’un code basique à écrire une fonction générale qui pourra être utilisée pour dessiner toutes mes zelliges.

Cette étoile comprend 16 segments et 16 sommets répartis en deux séries alternées d’angles convexes et d’angles concaves. On parle en mathématique, je pense, de polygone concave étoilé car si on prolonge un coté du polygone par une droite et si une de ces droites divise notre polygone (c’est-à-dire que notre polygone n’est pas d’un seul coté de cette droite, sur un demi-plan) alors le motif est concave et étoilé.

Pour l’exemple, j’ai pris comme position de ces sommets 250 points pour les angles aigus et 191,342 points pour les angles obtus. Cette forme est géométriquement exacte comme pièce de zellige. Les angles sont de 90 degrés pour les convexes et à 135 degrés pour les concaves.

Le rapport entre ces deux valeurs si on considère que le cercle à 250 points représente le la 440 hz alors notre autre cercle à 191,342 points correspondrait à 336,761 hz… ce qui malheureusement ne tombe pas juste pour une note car nous sommes entre le mi (330 hz) et le fa (349 hz).

Cherchons l’erreur.

Je dessine donc une autre forme d’étoile avec des branches plus marquées. Les angles sont de 45 degrés et 90 degrés. Cette fois-ci j’observe une mesure de la position des sommets concaves à 132,433 points du centre et une fréquence 238,126 hz et là aussi j’ai un décalage de quelques hz et je suis entre le sib (233 hz) et le si (247 hz). En faisant un rapport entre la valeur calculée géométriquement et la valeur calculée en utilisant le la (440 hz pour 250 points) et ce pour les deux figures j’ai exactement le même décalage de environ 2 % (2,1642195 % à moins d’un milliardième près).

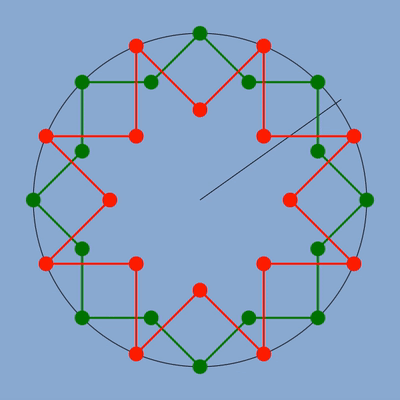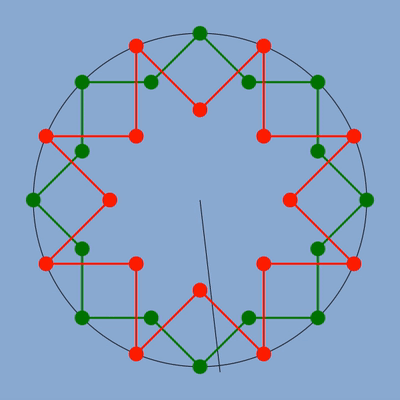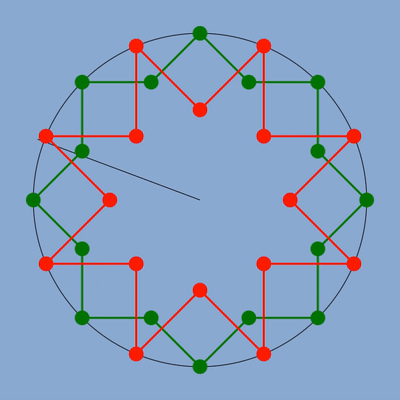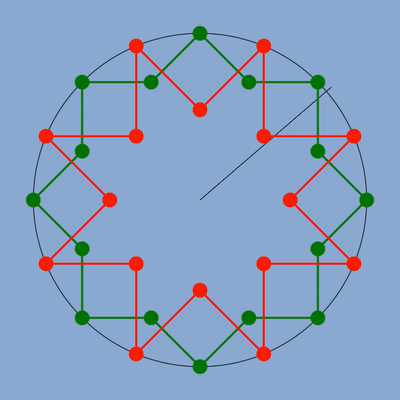
figure des deux étoiles calculées géométriquement

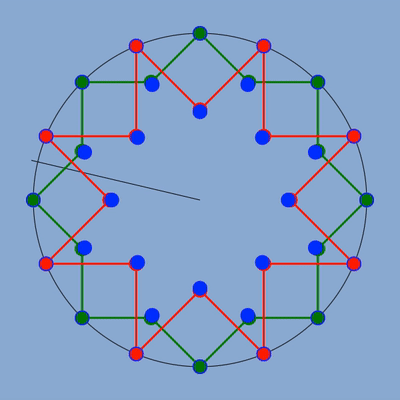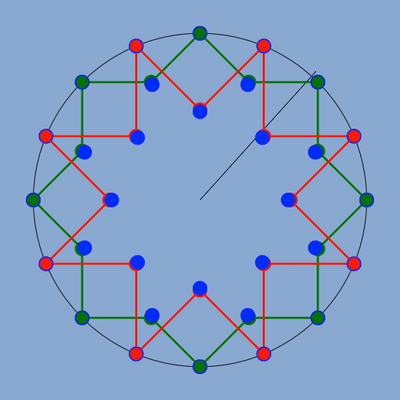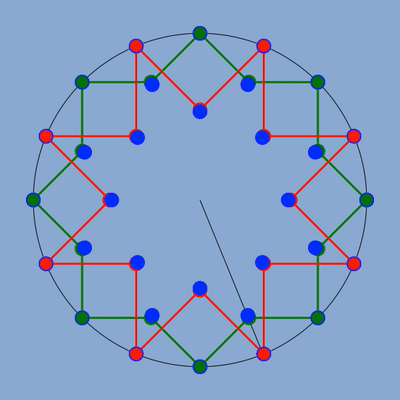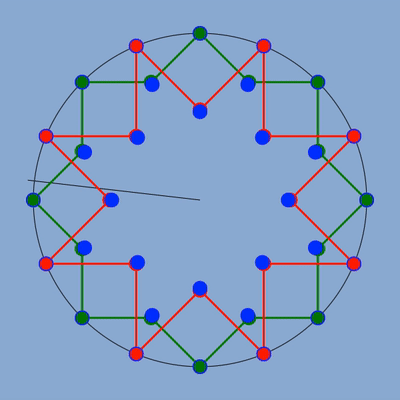
figure des deux étoiles avec en bleu la position des sommets qui respecterait la fréquence.

Si je réduis mon cercle de base (en gros ma référence au la du diapason) d’environ 2 % est-ce que je retomberai sur mes pattes ? Mes sommets correspondant au la seront donc à approximativement 244,704 points du centre.

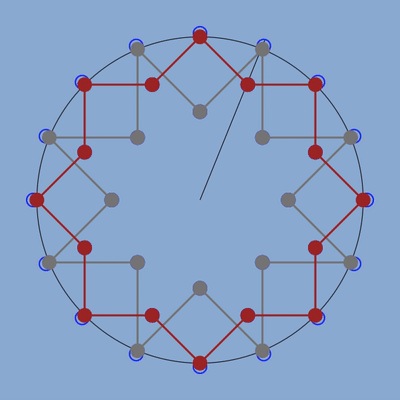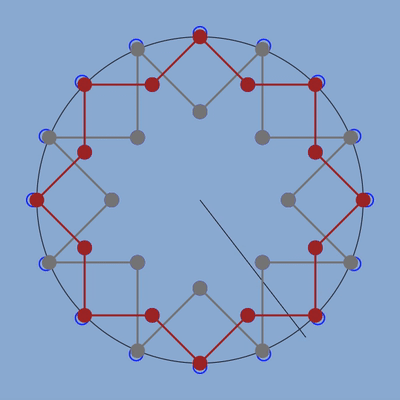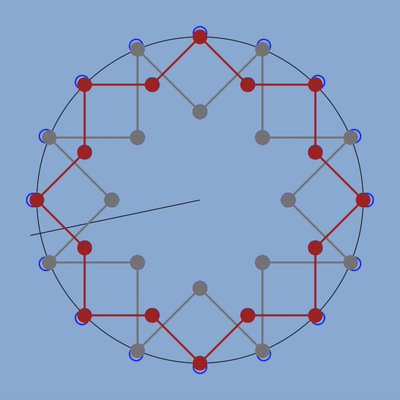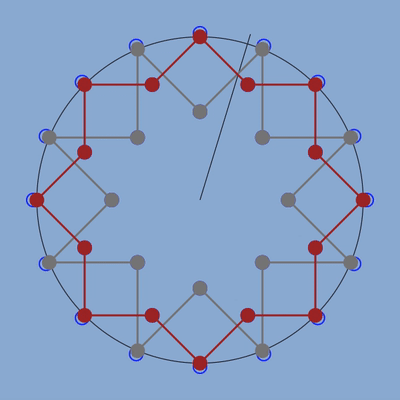
figure des deux étoiles avec en bleu la position des anciens points correspondant au la à 440 hz.

Je suis un peu étonné qu’en ne changeant que la position des sommets sur le cercle externe et correspondant normalement au la à 440 hz et en donnant aux autres notes les positions correspondant à leur fréquence juste dans la gamme des fréquences, l’ensemble du graphique se recale et les formes sont parfaites : angles, segments, tout a suivi.

Maintenant vient la vérification, Si la position de mes sommets est bonne alors j’ai tous mes segments de la même longueur et mes angles doivent être de 45, 90 et 135 degrés. C’est ok pour les segments à la vérification du théorème de Pythagore. Pour les angles, je dois utiliser la formule d’al-Kashi qui dit que pour un triangle quelconque ABC, je peux retrouver le coté BC en connaissant AB et AC et l’angle BAC. Ce théorème est sous la forme suivante :

a2 = b2 + c2 – 2bc * cos(BAC)

et donc pour trouver l’angle on réarrange l’ensemble comme ceci

cos(BAC) = (a2 – b2 – c2) /  -2bc.

Pour déterminer ce cosinus on a besoin de la position du sommet sur lequel se situe l’angle (A) et les deux positions des sommets adjacents (B et C). On sait que les segments AB et AC sont identiques puisqu’il s’agit de deux des segments de notre étoile. Il ne nous manque que le segment BC qu’on peut de nouveau retrouver par le Théorème de Pythagore ou la formule d’al-Kashi mais plus simple encore comme on sait qu’il y a alternance de 2 angles il suffit de trouver comment arriver à 360°. On a 16 points mais 8 motifs identiques comportant 2 angles. Dans les deux étoiles, on a un angle de 90° visible sur notre exemple. 360° est égal à 8 fois 45°. Donc comme on a un angle aigu et un angle obtus (ou concave et convexe) et que l’un des angles est à 90° le deuxième est obligatoirement le résultat de (90 – 45) ou (90 + 45), on obtient dans les deux cas 45 et 135 , le deuxième angle est donc de 45 ou de 135°. Normalement la formule d’al-Kashi nous prouverait cela mais si vous savez déjà que tous vos segments sont identiques, je ne pense pas qu’il y ait besoin de recalculer pour chaque angle à chaque sommet cette vérification d’autant plus que les sommets sont déjà calculés et les valeurs des angles à 90° sont confirmées par les valeurs des positions de ces sommets.

je dessinerai les autres formes de zelliges et je continuerai afin de voir si ces approximations se rencontrent sur d’autres pièces.

Bon maintenant un autre problème se pose.

J’ai diminué mon cercle extérieur d’environ 2% et donc mes sommets ne sont plus à 250 points du centre mais à 244,704 points. En terme de fréquence qu’est-ce que cela implique ? Si 250 points représente 440 hz alors 244,704 points représente 430,68 hz. Peut-on en déduire quelque chose ? 430,68 hz est très proche de 432 hz ! Par contre je base le calcul des autres fréquences sur 440 hz et les sommets sont bien placés mais si je change pour un diapason à 432 hz qu’est-ce que cela sous entend en terme de fréquence des notes ? Si je dois aussi les recalculer, il y aura de nouveau un décalage des sommets et je devrai baisser de nouveau la fréquence de mon diapason. Bref c’est comme le chien qui court après sa queue.

Je vous laisse réfléchir à cela et si vous avez une réponse à me donner, n’hésitez pas à m’écrire, je me suis peut-être trompé quelque part.

Malgré ce « problème », j’ai pu démontrer dans l’ensemble qu’il y a un rapport réel entre les notes de musique et les pièces de zelliges. Il me faut maintenant travailler à élaborer quelque chose de plus complet et intéressant musicalement.

Je parlerai dans un prochain article des rythmes euclidiens et du rapport avec ce travail. En attendant un peu de musique avec cet aperçu musical des formes qu’on vient de voir.